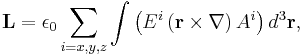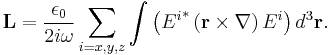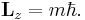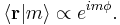Light orbital angular momentum
The light orbital angular momentum (OAM) is the component of angular momentum of a light beam that is dependent on the field spatial distribution, and not on the polarization. It can be further split into an internal and an external OAM. The internal OAM is an origin-independent angular momentum of a light beam that can be associated with a helical or twisted wavefront. The external OAM is the origin-dependent angular momentum that can be obtained as cross product of the light beam position (center of the beam) and its total linear momentum.
Contents |
Introduction
A beam of light carries a linear momentum 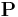 , and hence it can be also attributed an external angular momentum
, and hence it can be also attributed an external angular momentum 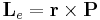 . This external angular momentum depends on the choice of the origin of the coordinate system. If one chooses the origin at the beam axis and the beam is cylindrically symmetric (at least in its momentum distribution), the external angular momentum will vanish. The external angular momentum is a form of OAM, because it is unrelated with polarization and depends on the spatial distribution of the optical field. A more interesting example of OAM is the internal OAM appearing when a paraxial light beam is in a so-called “helical mode”. Helical modes of the electromagnetic field are characterized by a wavefront that is shaped as a helix, with an optical vortex in the center, at the beam axis (see figure). The helical modes are characterized by an integer number
. This external angular momentum depends on the choice of the origin of the coordinate system. If one chooses the origin at the beam axis and the beam is cylindrically symmetric (at least in its momentum distribution), the external angular momentum will vanish. The external angular momentum is a form of OAM, because it is unrelated with polarization and depends on the spatial distribution of the optical field. A more interesting example of OAM is the internal OAM appearing when a paraxial light beam is in a so-called “helical mode”. Helical modes of the electromagnetic field are characterized by a wavefront that is shaped as a helix, with an optical vortex in the center, at the beam axis (see figure). The helical modes are characterized by an integer number  , positive or negative. If
, positive or negative. If 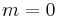 , the mode is not helical and the wavefronts are multiple disconnected surfaces, for example a sequence of parallel planes (from which the name “plane wave”). If
, the mode is not helical and the wavefronts are multiple disconnected surfaces, for example a sequence of parallel planes (from which the name “plane wave”). If 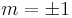 , the handedness determined by the sign of
, the handedness determined by the sign of  . If
. If 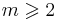 , the wavefront is shaped as
, the wavefront is shaped as 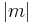 distinct wavefront is a single helical surface, with a step length equal to the wavelength
distinct wavefront is a single helical surface, with a step length equal to the wavelength  , and a still intertwined helices, with a step length of each helix surface equal to
, and a still intertwined helices, with a step length of each helix surface equal to 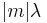 , and a handedness given by the sign of
, and a handedness given by the sign of  . The integer
. The integer  is also the so-called “topological charge” of the optical vortex. Light beams that are in a helical mode carry nonzero OAM.
is also the so-called “topological charge” of the optical vortex. Light beams that are in a helical mode carry nonzero OAM.
In this figure, the first column shows the beam wavefront shape. The second column is the optical phase distribution in a beam cross-section, shown in false colors. The third column is the light intensity distribution in a beam cross-section (with a dark vortex core at the center).
The beam photons in this case have an OAM of 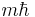 directed along the beam axis. This OAM is origin-independent.
directed along the beam axis. This OAM is origin-independent.
An example of optical modes having a helical wavefront is provided by the set of Laguerre-Gaussian modes.[1]
Mathematical expressions for the orbital angular momentum of light
The classical expression of the orbital angular momentum in the paraxial limit is the following[2]:
where 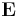 and
and 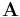 are the electric field and the vector potential, respectively,
are the electric field and the vector potential, respectively, 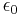 is the vacuum permittivity and we are using SI units. The
is the vacuum permittivity and we are using SI units. The  -superscripted symbols denote the cartesian components of the corresponding vectors.
-superscripted symbols denote the cartesian components of the corresponding vectors.
For a monochromatic wave this expression can be transformed into the following one[3] :
This expression is generally nonvanishing when the wave is not cylindrically symmetric. In particular, in a quantum theory, individual photons may have the following values of the OAM:
The corresponding wave functions (eigenfunctions of OAM operator) have the following general expression:
where  is the cylindrical coordinate. As mentioned in the Introduction, this expression corresponds to waves having a helical wavefront (see figure above), with an optical vortex in the center, at the beam axis.
is the cylindrical coordinate. As mentioned in the Introduction, this expression corresponds to waves having a helical wavefront (see figure above), with an optical vortex in the center, at the beam axis.
See also
References
- ^ Siegmam, Anthony E. (1986). Lasers. University Science Books. pp. 1283. ISBN 0935702113.
- ^ Belintante, F. J. (1940). "On the current and the density of the electric charge, the energy, the linear momentum and the angular momentum of arbitrary fields". Physica 7 (5): 449. doi:10.1016/S0031-8914(40)90091-X.
- ^ Humblet, J. (1943). "Sur le moment d'impulsion d'une onde electromagnetique". Physica (Utrecht) 10 (7): 585. doi:10.1016/S0031-8914(43)90626-3.
External links
- Phorbitech
- Glasgow Optics Group
- Leiden Institute of Physics
- ICFO
- Università Di Napoli "Federico II"
- Università Di Roma "La Sapienza"